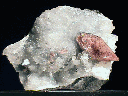
Vanadinite

THE HEXAGONAL SYSTEM

class name, number, symmetry
Dihexagonal Dipyramidal Class, 20th, 6/m 2/m 2/m
Hexagonal Trapezohedral Class, 19th, 6 2 2
Dihexagonal Pyramidal Class, 18th, 6 m m
Ditrigonal Dipyramidal Class, 17th, bar 6 m 2
Hexagonal Dipyramidal Class, 16th, 6/m
Trigonal Dipyramidal Class, 15th, bar 6
Hexagonal Pyramidal Class, 14th, 6

SOME HEXAGONAL MINERALS

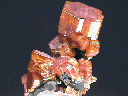
HANKSITE	THAUMASITE	VANADINITE
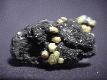
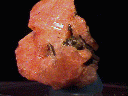
APATITE	ETTRINGITE	MOLYBDENITE
GMELINITE	AQUAMARINE	PYRRHOTITE

The hexagonal system is uniaxial, meaning it is based on one major axis, in this case a six fold rotational axis, that is unique to the other axes. The hexagonal system is analogous to the tetragonal system. The hexagonal system contains classes that mirror the tetragonal system's classes with the obvious difference being the six fold axis instead of the four fold axis.

However, the hexagonal system and the similar trigonal system are unlike any of the other five systems in terms of crystallographic axes. While the other systems use three crystallographic axes, the hexagonal and trigonal systems use a total of four axes. The major or principle six fold axis for the hexagonal system is, of course, one of the axes. The other three axes lie in a plane perpendicular to the principle axis and are labeled a₁, a₂ and a₃. These axes are symmetrically spread out to 120 degrees between the positive ends of each axis, making a six rayed star when viewed down the principle axis. In the hexagonal system there is no difference between the positive and negative poles of each a axis making a angle of only 60 degrees between the axes. However, if there exists a difference between the poles of the axes, then this would make the system trigonal, with a three fold principle axis, as opposed to hexagonal.

One item to note, it is now common practice among crystallographers to ignore one of the three perpendicular axes. Discussion of this fact may be more confusing than helpful, but here it goes. Since there are three equal axes, the system can actually be defined mathematically with only two perpendicular axes at 120 and 60 degree angles. The resulting pattern perpendicular to the c axis is a rhombus tiled mosaic that looks orthorhombic, not hexagonal. However, if the third axis is put in place connecting each junction of the first two axes and splitting the rhombus into two equilateral triangles, then the pattern clearly becomes hexagonal.

The highest symmetry class of the hexagonal system is the Dihexagonal Dipyramidal Class. In addition to the six fold axis, there are 6 axes of two fold rotation perpendicular to the principle axis, 7 mirror planes and a center. The three planar crystallographic axes represent three of the two fold axes and the other three two fold axes are positioned between the crystallographic axes. Thus there is only 30 degrees separating each two fold axis. There are 6 mirror planes that are all parallel to the principle axis and one two fold axis and perpendicular to one two fold axis. The other mirror plane lies in the plane occupied by the two fold axes. In addition there is a center of symmetry. This could arguably be called the most complex class of all the 32 different symmetry classes. Several minerals crystalize in this class and form some wonderfully symmetrical crystals.

The Hexagonal Trapezohedral Class has all the rotational axes of the Dihexagonal Dipyramidal Class but lacks the mirror planes and the center. The typical form looks like a dipyramid, but, without the mirrors, the faces do not line up evenly where they meet in the center of the crystal.

The Dihexagonal Pyramidal Class lacks the perpendicular mirror and the two fold axes. It is one of the few classes that produce a hemimorphic crystal, one that has a different shaped top and bottom. This occurs because there are no symmetry elements to repeat faces from the top to the bottom. A crystal from this class, such as from zincite, can have a symmetrical pyramid on the top and a basal pinacoid on the bottom.

Both the Ditrigonal Dipyramidal Class and the Trigonal Dipyramidal Class have 1 six fold rotoinversion axis (which appears as a three fold axes). The rotoinversion axis takes a face, rotates it 60 degrees (one sixth of a rotation) and then inverts it (up to down & right to left) through the crystal to the other side. Then it rotates it again 60 degrees and inverts it again through the crystal. Another four times through the rotoinversion operation (six in all) and it is back exactly where it started. The result is a trigonal looking crystal, although it was produced by a six fold rotational operation, thus the two classes belong in the hexagonal system.

The last class to discuss is the Hexagonal Dipyramidal Class. It only contains the six fold axis of rotation required for this system, a perpendicular mirror plane and a center. Crystals of this class are usually represented by members of the apatite group. These minerals show classic six fold symmetry and only occasionally show an offset face of the 12 sided hexagonal dipyramid.

Dihexagonal Dipyramidal Class

BERYL, variety Heliodor

Class: 20th
Symmetry: 6/m 2/m 2/m
Symmetry Elements: There is 1 six fold axis, 6 two fold axes, 7 mirror planes each perpendicular to one of the rotational axes and a center.
Crystallographic Axes: Three axes, all in one plane, termed a1, a2 and a3 are equal to each other, but they are either shorter or longer than the c axis.
Angles: All angles between the positive ends of the a axes = 120 degrees. The angle between all the a axes and the c axis = 90 degrees.
Common Forms: The dihexagonal dipyramid, hexagonal dipyramid, dihexagonal prism, hexagonal prism and the basal pinacoid.
Most Common Minerals Known to this Class: Beryl, molybdenite, pyrrhotite, nickeline, cancrinite, covellite, graphite cacoxenite, coquimbite, cordylite-(Ce), ettringite, fluocerite-(Ce), gmelinite, hauckite, osumilite, poudretteite, sjogrenite, sudburyite, sugilite, troilite, vaterite, zinc and even ice, among many others.

Hexagonal Trapezohedral Class

RHABDOPHANE

Class: 19th
Symmetry: 6 2 2
Symmetry Elements: There is 1 six fold axis and 6 two fold axes.
Crystallographic Axes: Three axes, all in one plane, termed a1, a2 and a3 are equal to each other, but they are either shorter or longer than the c axis.
Angles: All angles between the positive ends of the a axes = 120 degrees. The angle between all the a axes and the c axis = 90 degrees.
Of Note: Crystals can be left or right handed.
Common Forms: The hexagonal trapezohedron, hexagonal dipyramid, dihexagonal prism, hexagonal prism and the pinacoid.
Minerals Known to this Class: Rhabdophane, quetzalcoatlite, quintinite-2H and beta quartz or high quartz and about a dozen other rare minerals.

Dihexagonal Pyramidal Class

WURTZITE

Class: 18th
Symmetry: 6 m m
Symmetry Elements: There is 1 six fold axis and 6 mirror planes.
Crystallographic Axes: Three axes, all in one plane, termed a1, a2 and a3 are equal to each other, but they are either shorter or longer than the c axis.
Angles: All angles between the positive ends of the a axes = 120 degrees. The angle between all the a axes and the c axis = 90 degrees.
Of Note: Crystals of this group are hemimorphic, ie. different top and bottom.
Common Forms: The dihexagonal pyramid, hexagonal pyramid, dihexagonal prism, hexagonal prism and the pedion.
Most Common Minerals Known to this Class: Zincite, moissanite, taaffeite, greenockite and wurtzite as well as just a handfull of other rare minerals.

Ditrigonal Dipyramidal Class

BENITOITE

Class: 17th
Symmetry: Bar 6 m 2
Symmetry Elements: There is 1 six fold rotoinversion axis (appears as a three fold axes), 3 two fold axes and 4 mirror planes each perpendicular to one of the rotational axes.
Crystallographic Axes: Three axes, all in one plane, termed a1, a2 and a3 are equal to each other, but they are either shorter or longer than the c axis.
Angles: All angles between the positive ends of the a axes = 120 degrees. The angle between all the a axes and the c axis = 90 degrees.
Of Note: Crystals from this class appear to be trigonal.
Common Forms: The dihexagonal pyramid, hexagonal pyramid, dihexagonal prism, hexagonal prism and the pedion.
Minerals Known to this Class: Benitoite, belkovite, connellite, barringerite, bastnasite, hydroxylbastnasite, offretite and approximately ten even rarer minerals.

Hexagonal Dipyramidal Class

APATITE

Class: 16th
Symmetry: 6/m
Symmetry Elements: There is 1 six fold axis, 1 mirror plane perpendicular to the major rotational axes and a center.
Crystallographic Axes: Three axes, all in one plane, termed a1, a2 and a3 are equal to each other, but they are either shorter or longer than the c axis.
Angles: All angles between the positive ends of the a axes = 120 degrees. The angle between all the a axes and the c axis = 90 degrees.
Common Forms: The hexagonal dipyramid, hexagonal prism and the basal pinacoid.
Most Common Minerals Known to this Class: Agardite, hanksite, hedyphane, mixite, thaumasite and most members of the apatite group which includes the minerals apatite, mimetite, vanadinite and pyromorphite as well as a few rarer minerals.

Trigonal Dipyramidal Class

Class: 15th
Symmetry: Bar 6, equivalent to a 3/m
Symmetry Elements: There is 1 six fold rotoinversion axis (appears as a three fold axes) and 1 mirror plane perpendicular to the rotational axis.
Crystallographic Axes: Three axes, all in one plane, termed a1, a2 and a3 are equal to each other, but they are either shorter or longer than the c axis.
Angles: All angles between the positive ends of the a axes = 120 degrees. The angle between all the a axes and the c axis = 90 degrees.
Of Note: Crystals from this class appear to be trigonal.
Common Forms: The trigonal dipyramid, trigonal prism and the basal pinacoid.
Only Minerals Known to this Class: Only the very rare minerals Laurelite, liottite and reederite-(Y)

Hexagonal Pyramidal Class

Class: 14th
Symmetry: 6
Symmetry Elements: There is only 1 six fold axis.
Crystallographic Axes: Three axes, all in one plane, termed a1, a2 and a3 are equal to each other, but they are either shorter or longer than the c axis.
Angles: All angles between the positive ends of the a axes = 120 degrees. The angle between all the a axes and the c axis = 90 degrees.
Of Note: Crystals of this group are hemimorphic, ie. different top and bottom.
Common Forms: The hexagonal pyramid, hexagonal prism and the pedion.
Most Common Minerals Known to this Class: Nepheline, cancrinite, erionite, berthierite and gyrolite are the only somewhat common minerals known to this class. About 20 other very rare minerals also belong to this class.

Amethyst Galleries'
Mineral Gallery
MINERALS

Birthstones
Gemstones
By Name
Framed
Unframed
By Class: Carbonates; Elements; Halides; Oxides; Phosphates; Silicates; Sulfates; Sulfides
Fluorescent Minerals
Properties
Rocks
Search
Books

CRYSTAL SYMMETRY EXAMPLES
ISOMETRIC SPINEL
TETRAGONAL AUTUNITE
HEXAGONAL HANKSITE
TRIGONAL DIOPTASE
ORTHORHOMBIC CERUSSITE
MONOCLINIC HEULANDITE
TRICLINIC MICROCLINE
AMORPHOUS PRECIOUS OPAL