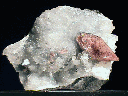
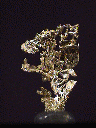SOME ISOMETRIC
MINERALS

SPINEL

LAZURITE

ANALCIME

GALENA
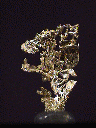
GOLD

FLUORITE

ALMANDINE

HALITE

COBALTITE

DIAMOND

TETRAHEDRITE

BIXBYITE
|
The isometric system is the most symmetrical system possible in
three dimensional space. It is composed of three crystallographic axes
of equal length and at right angles to each other. It differs from the
other systems in many ways. Isometric crystals do not polarize light as
it passes through them, making them more similar, in this case, to
amorphous
substances such as glass. In addition, the crystallographic axes, while
they do serve as some of the symmetry elements, are not the principle axes
of symmetry, as is true in the other systems. All the
isometric
crystal forms are closed forms and exclusive to this system. No isometric
crystals will have faces that belong to pyramids, prisms, rhombohedrons,
scalahedrons, domes, sphenoids, pinacoids or pedions.
The word, isometric, means "same measure", an allusion to the equal
three dimensional structure. "Cubic System" is a synonym for the isometric
system and is due to the cubic nature of the crystallographic structure
as well as the most common isometric form, the cube.
The most symmetrical class of all is the Hexoctahedral Class.
The three identical crystallographic axes serve as four fold rotational axes with
a square outline when viewed down each axis. However the principle and
defining axes for the isometric system are the 4 three fold axes. They
dissect the three crystallographic axes and are essentially the 4 diagonal
lines through a cube. If you picture a transparent cube, then draw lines
from each corner, through the middle to the other corner, then you will
end up with 4 lines that represent the 4 three fold axes. The three fold
rotational axes can be see on a cube as the axes through the three top
faces and the three bottom faces, when the cube is held from corner to
opposite corner.
The octahedron shows the three fold rotations better than the cube with
its triangular faces that are perpendicular to the three fold axes. The
four fold rotations though are not as easy to see on the octahedron, but
a square cross-section can be seen when viewed down the points of the octahedron.
The other forms of the hexoctahedral class all demonstrate these symmetry
elements including the 6 two fold axes and 9 mirror planes.
The Hextetrahedral Class lacks the 3 simple four fold rotational
axes because they are four fold rotoinversion axes. A four fold rotoinversion
axis takes a face, rotates it 90 degrees (one fourth of a rotation)
and then inverts it (up to down & right to left) through the crystal
to the other side. Then it rotates it again 90 degrees and inverts it again
through the crystal. Another rotoinversion operation and finally another
(four in all) and the face is back, exactly where it started. The crystal
then looks as if it has only two fold axes instead of the four fold axes
that it actually has. The hextetrahedral class produces a very symmetrical
tetrahedron and derivatives of this form. The three fold axes are very
easy to see in this class as they run through the triangular bases
and out the three faced pyramidal top. Of course there are no
bases or pyramids in the isometrmic system these terms are used only as
a visual guide to the shape of the tetrahedron.
The Gyroidal Class has all axes of the hexoctahedral class but
none of the mirror planes. This class produces a unique form called the
gyroid.
It has 24 faces that are in the shape of distorted pentagons. The lack
of mirror planes is clearly seen on the gyroid. This class like the other
classes can have forms that appear to be of higher symmetry such as the
cube. But etchings on crystal faces or other factors such as striations
can be used to reveal the true symmetry of the crystal.
The Diploidal Class lacks any four fold rotational axes or any
four fold rotoinversion axes. Remember, the isometric system doesn't require
four fold rotational axes. There is the required 4 three fold axes as well
as 3 two fold axes (parallel to the crystallographic axes), three mirrors
and a center. The class contains a few rare minerals and one very common,
well known and usually well crystallized mineral, that being
pyrite.
Pyrite lends its name to the classic form that comes from this class and
the form that pyrite is famous for, the
pyritohedron.
Although pyrite can form clean perfect cubes, it usually forms cubes that
are striated with fine grooves that run across the cube faces. The striations
are the result of the pyrite crystal trying to express its other form,
the pyritohedron. A careful examination of the pyritohedron and a cube
show that the cube faces and six of the edges on the pyritohedron are aligned
crystallographically. Therefore the edges imprint on the cube face as striations.
These striations ruin the cube's normal four fold axis that would have
entered the crystal in the middle of the cube face and this proves that
pyrite belongs to the Diploidal Class.
The lowest symmetry class in the isometric system is the
Tetartoidal Class. It lacks any mirror planes or a center, but has the required
4 three fold axes in addition to 3 two fold axes that lie on the crystallographic
axes. The tetartoid is a unique form and is a 12 sided form that peripherally
resembles the shape of a tetrahedron.

Fluorite
-
Class: 32nd
-
Symmetry: 4/m bar 3 2/m
-
Symmetry Elements: This is the most symmetrical possibility for
a three dimensional system with 4 three fold axes, 3 four fold axes and
6 two fold axes as well as 9 mirror planes and a center.
-
Crystallographic Axes: Three equal axes termed a1,
a2 and a3.
-
Angles: All three angles = 90 degrees.
-
Common Forms: The cube,
octahedron,
dodecahedron
and trapezohedron,
more rarely the trisoctahedron,
tetrahexahedron
andhexoctahedron.
-
Most Common Minerals:
Fluorite,
galena,
diamond,
copper,
iron,
lead,
platinum,
silver,
gold,
halite,
bromargyrite,
chlorargyrite,
moschellandsbergite,
murdochite,
osbornite,
periclase,
pollucite,
villiaumite,
pyrochlore,
thorianite,
the garnet group,
uraninite,
most members of the
spinel group,
pentlandite,
sylvite,
analcime and many others.
^

Sphalerite
-
Class: 31st
-
Symmetry: Bar 4 3 m
-
Symmetry Elements: There are 4 three fold axes, 3 four fold rotoinversion
axes (they appear as two fold axes) and 6 mirror planes.
-
Crystallographic Axes: Three equal axes termed a1,
a2 and a3.
-
Angles: All three angles = 90 degrees.
-
Common Forms: The
tetrahedron,
tristetrahedron,
deltoidal dodecahedron
and hextetrahedron,
and more rarely the cube,
rhombic dodecahedron and
tetrahexahedron.
-
Most Common Minerals:
Sodalite,
sphalerite,
domeykite,
hauyne,
zunyite,
helvite,
metacinnabar,
hawleyite,
lazurite,
rhodizite,
tetrahedriteand
tennantite
along with several other rare minerals.
^

Cuprite
-
Class: 30th
-
Symmetry: 4 3 2
-
Symmetry Elements: There are 3 four fold axes, 4 three fold axes
and 6 two fold axes.
-
Crystallographic Axes: Three equal axes termed a1,
a2 and a3.
-
Angles: All three angles = 90 degrees.
-
Of Note: Crystals can be left or right handed.
-
Common Forms: The unique gyroid form
as well as the cube,
octahedron,
dodecahedron and
trapezohedron,
more rarely the
trisoctahedron and
tetrahexahedron.
-
Most Common Minerals:
Lawsonite,
petzite,
fischesserite,
sakhaite and
yeelimite.
The minerals cuprite,
voltaite and
sal ammoniac
are in dispute as to belonging to this class, but sometimes show crystal forms consistent with this class.
^

Pyrite
- Class: 29th
- Symmetry: 2/m bar 3
-
Symmetry Elements: There are 4 three fold axes, 3 two fold axes,
3 mirror planes and a center.
-
Crystallographic Axes: Three equal axes termed a1,
a2 and a3.
-
Angles: All three angles = 90 degrees.
-
Common Forms: The unique diploid and
pyritohedron
as well as the cube,
octahedron,
rhombic dodecahedron,
trapezohedron and more rarely the
trisoctahedron.
-
Most Common Minerals: Pyrite,
cobaltite,
cliffordite,
hauerite,
ullmannite,
penroseite,
tychite,
laurite,
skutterudite,
bixbyite and
sperrylite.
^

- Class: 28th
- Symmetry: 2 3
-
Symmetry Elements: There are 4 three fold axes and 3 two fold axes.
-
Crystallographic Axes: Three equal axes termed a1,
a2 and a3.
-
Angles: All three angles = 90 degrees.
-
Of Note: Crystals can be left or right handed, enantiomorphic.
-
Common Forms: The unique tetartoid
as well as the pyritohedron,
cube,
deltoidal dodecahedron,
pentagonal dodecahedron,
rhombic dodecahedronand the
tetrahedron.
-
Most Common Minerals Known to this Class: Include very rare minerals such as
Changchengite,
corderoite,
gersdorffite,
langbeinite,
maghemite,
michenerite,
pharmacosiderite,
ullmannite (higher ordered)
and a few other very rare minerals.
^
|