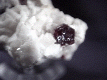
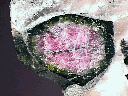
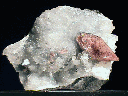
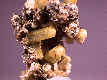Siderite |
Isometric | Tetragonal | Hexagonal | Orthorhombic | Monoclinic | Triclinic | THE TRIGONAL SYSTEM
|
|
MINERALS
|
The trigonal system is sometimes included in the
hexagonal system as a division, called the rhombohedral division with the other hexagonal classes grouped into the hexagonal division.
However, the difference between the two divisions is large enough to merit dividing the two into two distinctive systems, albeit acknowledging their close similarities.
The hexagonal system has as its defining characteristic a six fold rotational axis or a six fold rotoinversion axis.
The trigonal system likewise has a three fold rotational axis or a three fold rotoinversion axis.
Although the six fold rotoinversion axis produces a trigonal looking crystal, that symmetry is produced by the six fold symmetry operation.
Also the classes of the trigonal system frequently use forms "belonging" to the hexagonal system.
But this kind of borrowing is allowed as
orthorhombic classes "borrow" domes, sphenoids and pinacoids from the monoclinic system.
The hexagonal and trigonal systems are unlike any of the other systems in terms of crystallographic axes. While the other systems use three crystallographic axes, the hexagonal and trigonal systems use four axes. The major or principle three fold or six fold axis is, of course, one of the axes. The other three axes lie in a plane perpendicular to the principle axis. Modern crystallographers actually ignore one of these axes and use only two of the perpendicular axes to define the crystallography of this system, see the discussion of of this matter in the hexagonal system. The three perpendicular axes are symmetrically spread out with 120 degrees between the positive ends of each axis. If the axes are extended through the center, then the angle between each axes is only 60 degrees. In the hexagonal system there is no difference between the positive and negative poles of an axis. However, if there exists a difference between the poles of the axes, then this would make the system trigonal as opposed to hexagonal. The highest symmetry class in the trigonal system is the Hexagonal Scalenohedral Class. It has 1 three fold rotoinversion axis, 3 two fold axes, 3 mirror planes parallel to the principle axis and a center. This class, more so than the other classes of this system, has members that "borrow" forms from the more symmetrical hexagonal system's classes. In fact, unless a crystal from this class shows rhombohedral or scalenohedral faces or rhombohedral cleavage or parting, it will be difficult to determine the crystal's true symmetry. The Trigonal Trapezohedral Class has one of the most common minerals in the Earth's crust as its member. Quartz crystallizes in this class, but only outwardly shows its true symmetry occasionally with the small trapezohedral faces. The trapezohedral faces will modify the corner of the prism faces as the prism faces intersect the pyramid faces. The corner trapezohedral face is either in the right or left side of the prism and distinguishes a right handed quartz crystal from a left handed crystal. Both the Ditrigonal Pyramidal Class and Trigonal Pyramidal Class are hemimorphic which means they have a different top and bottom. A typical crystal, might have a pyramid top and a pedion for a base. In the case of tourmaline which belongs to the Ditrigonal Pyramidal Class, the top of the crystal might have a pyramid that is steep while the bottom might have a pyramid that is less inclined. Crystals from both classes could be hard to distinguish as the only difference is the presence or absence of mirror planes. The Rhombohedral Class only has a three fold rotoinversion axis. Unlike other rotoinversion axis with four fold or six fold rotations, the three fold rotoinversion axis does not appear to lower its own symmetry (see classes 15, 17, 22, 24 & 30). The three fold rotoinversion axis takes a face, rotates it 120 degrees (one third of a rotation) and then inverts it (up to down & right to left) through the crystal to the other side. Then it rotates it again 120 degrees and inverts it again through the crystal. Another four times through the rotoinversion operation (six in all) and it is back exactly where it started. The result is still a trigonal looking crystal (a rhombohedron for example) with six faces, three above and three below. The six fold rotoinversion differs from the three fold rotoinversion in the production of a perpendicular mirror plane. The six fold rotoinversion produces a perpendicular mirror plane because the top three faces are directly above the bottom three faces. But in the three fold rotoinversion the top three faces are rotated 60 degrees from the bottom three faces so that no perpendicular mirror plane can exist. Hexagonal Scalenohedral Class
Calcite
Trigonal Trapezohedral Class
Ditrigonal Pyramidal Class
Rhombohedral Class
Trigonal Pyramidal Class
|
|---|